왜 미-파 시-도 는 반음이냐.. 4:5:6 비율의 작품

첫글이다. 예전 공부할 때 실험실에 음향학을하는 친구들이 있었다. 음악이 주파와 밀접한 관계인것 머리로는 알겠는데.. 아직도 귀는 막귀다.. 그것이 도대체 무엇이길래..ㅜㅜ

현재 우리가 노래하는 도레미파솔라시도는 피타고라스라는 수학자에서 기인한다. (물론 이후에 바하라는 자가 대대적인 개편을 했지만..) 주말에 인터넷 여기저기 돌아다니는데 대부분  음악중심으로 서술되어 있어 그냥 바벼운 수학 중심으로 도레미파솔라시도를 살펴 보겠다.

피타고라스가 어느날 대장간 옆을 지나가는데 굉장히 좋은 화음이 들린다. 분석해 보니 주파수비가 2:3 일때 좋은 화음이 들리는걸 알았다. 도-솔 화음이다. 솔은 낮은도-높은도 의 중간음이다. 여기서 더 나가 그 중간음 2 : 2.5 : 3 즉 4 : 5 :6 도 훌륭한 화음을 만드는것을 발견한다.

여기서 잠깐 태클: 그 당시에는 주파수 개념이 없었음이 당연하다. 어찌 측정할 방법도 없고. 다만 쇠막대 길이가 2배가 되면 저음이지만 비슷한 소리가 나는걸 알았고 (이걸 옥타브라고 현재도 부른다). 그 사이에 적절한 음이 있어 조화를 이루는걸 알았는데.. 사실 주파수는 쇠막대 길이에 반비례한다. 따라서 쇠막대 길이의 역수비 즉 (1/2):(1/3) 길이비가 좋은 화음을 만들었음을 알았을 것이다..

그렇다 우리는 두 가지 정보만으로 음계를 만들어 보겠다

• 주파수 2배나 1/2배는 같은 가족이다 (옥타브)
• 좋은 화음은 4:5:6 이다

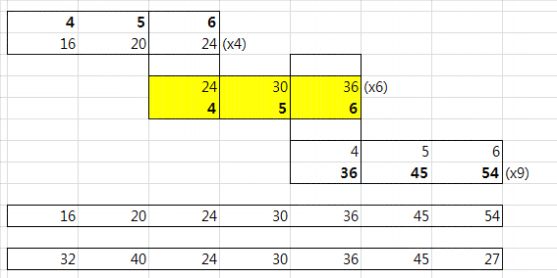
이것을 근거로 한 옥타브 안에 음계를 만들어 보자. 4:5:6을 현재에서 낮은쪽, 높음쪽 양쪽으로 다시 그 비율을 가지는 쌍을 만든다. 즉

위에서 처럼 (4:5:6) 비율 3개를 연결 시키면 16, 20, ...., 54 까지 7개의 숫자를 얻는다.  이제 한 옥타브에 집어 넣기위해 (24~ 48) 그것을 2를 곱하거나 2로 나눈다. (한 옥타브는 같은 가족이라고 했다) 그려면 24~48 사이에 있는 7개의 주파수가 나올 것이다. 이제 그것을 크기 순으로 다시 정렬한다.

그 숫자들이 곧 도레미파솔라시인 것이다. 여기서 잠시 눈여겨 볼것이 있다. "레"는 "도"보다 9/8 만큼 크다. 사실 온음이 다 같은차이는 아니고 9/8, 또는 10/9 다 (물론 바하가 창시한 현재 음계는 두개가 같다. 아주 이상한 숫자 만큼..) 그런데 미-파, 시-도 사이는 16/15 로 좀 작다. 반음이다. 정확히 말하면 "반"음은 아니다. 이것들은 나중에 바하라는 사람이 평균율 이라는 이름으로 재정비 된다. 정확히 반음, 정확히 온음을 지키는 음계로..각 반음의 비율은 정확히 2^(1/12) = 1.05946..... 만큼.  수학의 로그라는것을 좀 알아야 한다.  공부해라 이것들아..

PS: 실로폰을 직접만들고 싶다면.. 주파수는 길이에 반비례한다는 것도 참고..